En este otro post hablamos del trabajo de una forma más extensa. Partiendo de lo ya dicho en ese post:
Una fuerza es conservativa cuando el trabajo realizado a lo largo de una superficie cerrada es cero; es decir, el trabajo realizado no depende del camino seguido, sino de la posición inicial y final. Matemáticamente:
Veamos esto con dos ejemplos:
 |
A pesar de la trayectoria seguida, el trabajo realizado por la fuerza es el mismo (sólo depende de 1 y 2)
W(S1) = W(S2)
|
 |
| WTOTAL = W(C1) + W(C2); W(C1) = - W(C2) (porque son de sentido contrario) → WTOTAL = 0 |
La fuerza gravitatoria es un ejemplo de fuerza conservativa. Esto nos permite decir que la energía mecánica es, por lo tanto, constante:
Las fuerzas centrales son aquellas que están constantemente dirigidas hacia un mismo punto, independientemente de la posición de la partícula sobre la que está actuando. La fuerza gravitatoria, por ejemplo, es una fuerza central, así como la eléctrica o la centrípeta. Todas las fuerzas centrales son conservativas.
En estas fuerzas, por lo tanto, la fuerza (en negro) y el vector del radio (en rojo), forman 180º. Teniendo en cuenta esto, podemos pasar a demostrar que el momento angular en estas fuerzas (y, por lo tanto, en la gravitatoria), es constante.
Para ello tenemos el momento de una fuerza (también llamado "torque"), que ese define como:
siendo su módulo:
donde r es vector que une el origen O con el punto donde se encuentra el cuerpo de masa m y F es la fuerza que se le aplica. Su unidad de medida es el Newton-metro (N · m).
Igualmente, pasaremos a definir el momento angular de una partícula (imagen superior):
donde r es la distancia desde el punto O hasta donde se encuentra el cuerpo de masa m y p es su momento lineal: la masa multiplicada por su velocidad. En módulo:
Al mismo tiempo, se cumple que:
como se demuestra fácilmente:
pero como r es constante, tenemos que
por lo que
y, al mismo tiempo, tenemos que tener en cuenta que
que nos permite llegar a
Teniendo en cuenta la II Ley de Newton:
Obtenemos así la expresión buscada:
Partiendo de esta expresión ya estamos en condiciones de demostrar que en el campo gravitatorio el momento angular es constante:
Pero en el campo gravitatorio, como se puede ver en la primera imagen, los vectores de r y de F forman 180º, por lo que su producto vectorial (y, por lo tanto, el momento de la fuerza) es cero:
Al mismo tiempo, utilizando la relación entre el momento de la fuerza y el momento angular:
Por lo tanto, la derivada del momento angular debe ser cero, algo que sólo se consigue si el momento angular es constante (recordemos que la derivada de una constante es cero).
2. Vector intensidad campo gravitatorio
La
intensidad del campo gravitatorio en un punto es la fuerza que ejerce el campo
sobre la unidad de masa colocada en dicho punto. Puede considerarse,
igualmente, con la aceleración que experimenta un cuerpo en caída libre sobre el que lo atrae. Sin embargo, no debe confundirse con la aceleración de la gravedad, que es un campo gravitatorio concreto: el de la Tierra. Matemáticamente:
En notación vectorial:
El signo significa que el vector intensidad del campo gravitatorio tiene el mismo sentido que la fuerza de gravedad pero que éste es opuesto a ur, pues está dirigido hacia la masa que lo crea.
La unidad de medida de este vector es la misma que la de la aceleración: N/m = m/s2, y, como se ve, es una aceleración independiente de la masa del objeto.
A todo punto del espacio que rodea a la Tierra se le puede asociar un vector intensidad de campo gravitatorio terrestre, recibiendo el nombre de "aceleración de la gravedad". La dirección de este vector es la de la línea que une el objeto con la Tierra, y el sentido es hacia el centro de la Tierra.
La gravedad sobre la superficie es:
Por lo tanto, en el interior de la Tierra será:
Y, como se aprecia en la fórmula, disminuye con el cuadrado
de la distancia (sólo se anula en el infinito).
Por otra parte, la masa de la Tierra es:
Si
ahora tomamos la esfera del interior de la Tierra (en la imagen, la esfera roja), con un radio r < R; r = R - h tenemos que su masa es:
Dividiendo miembro a miembro ambas
expresiones (puesto que queremos quitarnos de encima 4/3, r y p):
Ahora sustituimos esto en la fórmula de la expresión de la gravedad en el interior (II):
De esta forma, llegamos a:
Y, desarrollando más (teniendo en cuenta (I)):
Otra expresión igualmente válida es (sabiendo que r = R - h):
Es decir, a medida que se
profundiza en el interior de la Tierra el valor de g disminuye, anulándose en el centro de la Tierra, donde h = R, como se ve en esta gráfica:
Para más información, puedes consultar aquí.
Se denomina potencial en un punto A del campo gravitatoria al trabajo realizado por la fuerza gravitatoria para trasladar la unidad de masa sometida a la acción del campo desde el infinito hasta dicho punto. Como se definirá a continuación la energía potencial, podemos tomarlo también como la energía potencial de un sistema entre la masa:
Y como V(∞) = 0, tenemos que:
4. Líneas de campo y superficies equipotenciales
Un campo de fuerzas, como es el gravitatorio, podemos representarlo por líneas de fuerza y superficies equipotenciales:
- Líneas de fuerza: En cada punto, el vector intensidad del campo gravitatorio es tangente a las líneas de campo y tiene el mismo sentido que éstas.
Por otra parte, han de trazarse de modo que la densidad de líneas de campo (número de líneas que atraviesan la unidad de superficie colocada perpendicularmente a éstas) sea proporcional al módulo del campo gravitatorio. El campo será más intenso, por lo tanto, en aquellas regiones en las que las líneas de campo estén más juntas.
- Líneas de fuerza: En cada punto, el vector intensidad del campo gravitatorio es tangente a las líneas de campo y tiene el mismo sentido que éstas.
Por otra parte, han de trazarse de modo que la densidad de líneas de campo (número de líneas que atraviesan la unidad de superficie colocada perpendicularmente a éstas) sea proporcional al módulo del campo gravitatorio. El campo será más intenso, por lo tanto, en aquellas regiones en las que las líneas de campo estén más juntas.
- Superficies equipotenciales: Al unir los puntos en los cuales el potencial gravitatorio tiene el mismo valor, podemos obtener una serie de superficies llamadas superficies equipotenciales. Éstas son perpendiculares a las líneas de campo en cualquier punto. Además, para un masa puntual, el potencial toma el mismo valor en todos los puntos situados a la misma distancia de la masa. Por lo tanto, las superficies equipotenciales son esferas concéntricas con el centro de la propia masa.
Esto, además, nos permite utilizar una expresión para el trabajo realizado por el campo:
En el caso de encontrarse A y B en la misma superficie equipotencial, va a cumplirse que el trabajo realizado por el campo es igual a cero:






























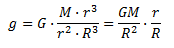











No hay comentarios:
Publicar un comentario